The slabtype algorithm, Part 4: Final layout and source code
Algorithms, Flash, Graphic Design, Interactive Design, Source Code, Typography,
1/30/08
This is the final installment of a four-part graphical dissection of the “slabtype” text layout algorithm I developed for Public Secrets. For an introduction to the algorithm, visit The slabtype algorithm, Part 1: Background. To review some calculations that set the stage, visit Part 2: Initial calculations. To get into the real meat of the algorithm, visit Part 3: Iterative line splitting.
In this post, we’ll wrap things up by doing our final layout of the text, followed by the source code for the algorithm. The iterative sequence we explored in the previous installment successfully turned our original text:

into seven separate lines:

We’re almost done. Our next task is to assemble these lines into a slab by scaling them all to an identical pixel width:

And finally, to scale the entire slab to fit inside the original box, allowing for a minimum amount of padding on each side:

And with that, the algorithm has run its course. In conjunction with the treemap algorithm, the slabtype algorithm allows us to dynamically lay out the entire contents of a screen like this

using only a collection of quotes as a starting point. Due to randomization in the input to the treemap algorithm, even identical collections of quotes are never laid out in exactly the same way. Within Public Secrets, you can briefly see the dynamism of the slabtype algorithm in action when a box containing a quote resizes as it moves from one location to another—the text inside shifts around to keep pace with the changing dimensions of its enclosing rectangle.
This algorithm was included in Public Secrets as a method called formatInscription, which is reproduced below (AS 2.0). I hope this has been a useful exercise—I’d love to get your feedback, questions, or suggestions for improvement.
/* — formatInscription : formats the text to fit the slab dimensions — */
public function formatInscription(rect:Rectangle, useMargin:Boolean):Void {
// calculate height of the ‘ideal’ line
var idealLineAspectRatio:Number = PS.fontInfo.altGoth3D.aspectRatio * PS.fontInfo.altGoth3D.idealLineLength;
var idealLineWidth:Number = rect.width;
var idealLineHeight:Number = idealLineWidth / idealLineAspectRatio;
var lineCount:Number = Math.floor(rect.height / idealLineHeight);
var idealCharPerLine:Number = Math.min(60, Math.max(Math.round(this._inscription.length / lineCount), 1));
// segment the text into lines
var words:Array = this._inscription.split(” ”);
var lineBreaks:Array = new Array();
var preText,postText,finalText:String;
var preDiff,postDiff:Number;
var wordIndex:Number = 0;
var lineText:Array = new Array();
var counter:Number = 0;
// while we still have words left, build the next line
while (wordIndex < words.length) {
postText = ”“;
// build two strings (preText and postText) word by word, with one
// string always one word behind the other, until
// the length of one string is less than the ideal number of characters
// per line, while the length of the other is greater than that ideal
while (postText.length < idealCharPerLine) {
preText = postText;
postText += words[wordIndex]+” ”;
wordIndex++;
if (wordIndex >= words.length) {
break;
}
}
// calculate the character difference between the two strings and the
// ideal number of characters per line
preDiff = idealCharPerLine - preText.length;
postDiff = postText.length - idealCharPerLine;
// if the smaller string is closer to the length of the ideal than
// the longer string, and doesn’t contain just a single space, then
// use that one for the line
if ((preDiff < postDiff) && (preText.length > 2)) {
finalText = preText;
wordIndex—;
// otherwise, use the longer string for the line
} else {
finalText = postText;
}
lineText.push(finalText.substr(0, finalText.length-1));
}
lineCount = lineText.length;
// create inscription clip
this._inscriptionClip.removeMovieClip();
this.createEmptyMovieClip(“inscriptionClip”, 10);
this._inscriptionClip = this[“inscriptionClip”];
// build the text fields
var curY:Number = 0;
this._lines = new Array();
for (var i:Number=0; i<lineCount; i++) {
this._inscriptionClip.attachMovie(“altGoth3DText”, “line”+i, 10+i);
this._lines.push(this._inscriptionClip[“line”+i]);
this._lines[i].content.text = lineText[i];
// scale this line so it exactly fits with width of the rect
this._lines[i]._yscale = this._lines[i]._xscale = (rect.width / this._lines[i].content.textWidth) * 100;
this._lines[i]._y = curY;
curY += this._lines[i]._height * .59;
}
this._inscriptionWidth = rect.width;
this._inscriptionHeight = curY;
this._inscriptionAR = this._inscriptionWidth / this._inscriptionHeight;
if (useMargin) {
var margin:Number = this._margin;
} else {
var margin:Number = 0;
}
// calculate the scaling to apply so the total inscription fits inside the rect
// centered, with the given margin
var clipScale:Number;
clipScale = ((rect.width-(margin * 2)) / rect.width) * 100;
if (this._inscriptionHeight > rect.height) {
clipScale = ((rect.height-(margin * 2)) / this._inscriptionHeight) * 100;
}
this._inscriptionClip._yscale = this._inscriptionClip._xscale = clipScale;
this._inscriptionClip._x = (rect.width - (rect.width * (clipScale / 100))) / 2;
this._inscriptionClip._y = (rect.height - (this._inscriptionHeight * (clipScale / 100))) / 2;
GraphicUtil.changeColor(this._inscriptionClip, this._colorScheme.text_color);
}
The slabtype algorithm, Part 3: Iterative line splitting
Algorithms, Flash, Graphic Design, Interactive Design, Typography,
1/28/08
This is the third in a four-part graphical dissection of the “slabtype” text layout algorithm I developed for Public Secrets. For an introduction to the algorithm, visit The slabtype algorithm, Part 1: Background. To review the calculations that set the stage for this post, visit Part 2: Initial calculations.
In this post, we’ll take up the real workhorse of the slabtype algorithm—iterative line splitting—followed by the final layout of the text.
Our initial calculations provided us with a single very important number: 8, our ideal character count per line. This number gives us a target to aim for as we split our text into individual lines. We start by dividing our text into its constituent words:

Next, we execute the following iterative sequence:
- Create two containers for words. One will hold the next word of the text, the other will hold the next two words of the text.
- Keep adding subsequent words to both containers until the character length of one container is less than or equal to the length of the ideal character count per line, while the character length of the other container is greater than the ideal character count per line.
- Store the contents of the container whose character count is closest to the ideal character count per line.
- Repeat.
Here’s a diagram of how we arrive at our first line using this sequence:

In this example, our two word containers initially hold the words “I and “I WISH. Neither of these exceed the ideal character count per line, so we continue adding words, giving us “I WISH and “I WISH IT. The latter is ten characters long, two characters longer than our ideal character count per line of eight. Since the former is seven characters long, resulting in only a one-character difference between its length and the ideal, we store “I WISH as the contents as the first line of the slab.
Here’s how we arrive at the next line:

Here, we have a very similar case. Neither IT nor IT WAS exceed the ideal character count, so we proceed to IT WAS and IT WAS THAT. IT WAS is only two characters off the ideal, compared to three characters for IT WAS THAT, so we pick the former.

The third line plays out a bit differently. With THAT and THAT SIMPLE, we find that THAT SIMPLE’s character count of eleven is nearer the target of eight than THAT’s character count of four, so we go with the latter.
The fourth line plays out much like the first two:

While the fifth pass chooses the first of the two text containers:

The sixth finds ERASE MY matching the ideal character count per line exactly:

Leaving PAST” as our only remaining word, which becomes a line unto itself.

Since we have exhausted our available words, the iterative part of the algorithm ends, resulting in our original text being split into seven lines:

For the final installment, we’ll turn our attention to laying out the text within the target box (source code will be provided).
Coming soon: The slabtype algorithm, Part 4: Final layout and source code
The slabtype algorithm, Part 2: Initial calculations
Algorithms, Flash, Graphic Design, Interactive Design, Typography,
1/24/08
This is the second in a four-part graphical dissection of the “slabtype” text layout algorithm I developed for Public Secrets. For an introduction to the algorithm, visit The slabtype algorithm, Part 1: Background.
Execution of the slabtype algorithm breaks down into three phases: initial calculations, iterative line splitting, and final layout. In this post, we’ll tackle the initial calculations that set the stage for the work of the algorithm.
Three constants are used to constrain the results of the initial calculations. The first is the average aspect ratio of a single character of the font we plan to use (Alternate Gothic No. 3, in this case). This is important because it gives us a way to guess how wide a particular line of text is going to be without consuming precious time by actually laying it out. I looked at a selection of characters from the font and estimated the aspect ratio accordingly.
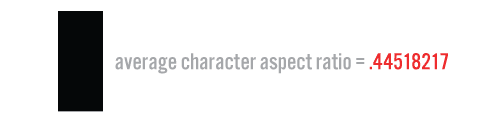
Next, I decided upon a character count for the “ideal line length” of text to be fit into the slab. Since I used the “squarified” variant of the treemap algorithm to generate the enclosing boxes, I could be confident that a fixed value would give good results, but a more truly dynamic implementation would derive the ideal line length from a pixel value for the average height or width of a single character in the ideal point size for the display.

We multiply the average character aspect ratio by the ideal line length to arrive at an aspect ratio for the “ideal line”:

These constants are defined once at the beginning of the program. The calculations which follow are executed each time the algorithm is invoked.
We start with the text which the algorithm is tasked with laying out.

The algorithm is then supplied with the dimensions of the slab (box) into which the text is to be placed:

We divide the width of the box by the aspect ratio of the “ideal line” of text which it is to contain, resulting in a pixel value for the height of this line.
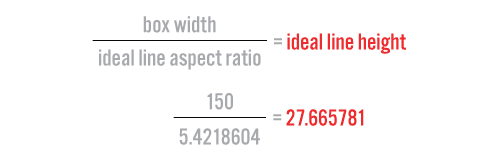
When we divide the height of the box by the height of the ideal line, we arrive at a hypothetical line count—an estimate of how many lines the text is going to have to be broken into to fit snugly within the box.
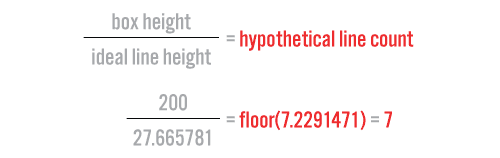
Since we know the number of characters in our text, we divide it by our hypothetical line count to come up with an “ideal character count” per line of text.
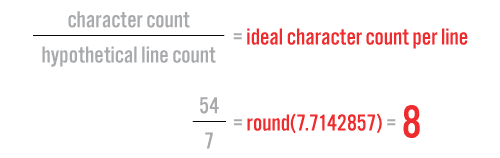
As we will see in the next part, this is a very important value—it becomes a benchmark to help us decide where to split the text into lines.
Coming soon: The slabtype algorithm, Part 3: Iterative line splitting
Recent Posts
Go InSight: Composing a Musical Summation of Every Mission to Mars (Part 2)
Making music out of the data of interplanetary exploration.
Go InSight: Composing a musical summation of every mission to Mars (Part 1)
Making music out of the data of interplanetary exploration.
Cited Works from “Storytelling in the Age of Divided Screens”
Here’s a list of links to works cited in my recent talk “Storytelling in the Age of Divided Screens” at Gallaudet University.
Timeframing: The Art of Comics on Screens
I’m very happy to announce the launch of “Timeframing: The Art of Comics on Screens,” a new website that explores what comics have to teach us about creative communication in the age of screen media.
The prototype that led to Upgrade Soul
To celebrate the launch of Upgrade Soul, here’s a screen shot of an eleven year old prototype I made that sets artwork from Will Eisner’s “The Treasure of Avenue ‘C’” (a story from New York: The Big City) in two dynamically resizable panels.
Categories
Algorithms
Animation
Announcements
Authoring Tools
Comics
Digital Humanities
Electronic Literature
Events
Experiments
Exemplary Work
Flash
Flex
Fun
Games
Graphic Design
Interactive Design
iPhone
jQuery
LA Flash
Miscellaneous
Music
Opertoon
Remembrances
Source Code
Typography
User Experience
Viewfinder
Wii
Archives
July 2018
May 2018
February 2015
October 2014
October 2012
February 2012
January 2012
January 2011
April 2010
March 2010
October 2009
February 2009
January 2009
December 2008
September 2008
July 2008
June 2008
April 2008
March 2008
February 2008
January 2008
November 2007
October 2007
September 2007
August 2007
July 2007
June 2007